jueves, 7 de noviembre de 2013

Algebra logica 



Partes: 1, 2

La disyunción es otro símbolo matemático perteneciente a los conectivos lógicos cuya representación es una (V) normal. También este conectivo tendrá su significado propio en las oraciones. La disyunción reemplazara la Vocal O en las proposiciones y por ende se llega a la conclusión de que el valor de (v) = O y se leerá tal como la vocal
  • c) Implicación (?)
La implicación es uno de los conectivos mas importantes ya que tiene mas valor que la conjuncion y la disyunción su simbología matemática es una flecha (?) es un conectivo que tiene varios significados y por ende habrá que prestarle un poco mas de atención. Reemplazara las palabras Entonces, Luego, Por ende. Por tanto Etc.
En las proposiciones y por ende se llega a la conclusión de que el símbolo (?) tendrá varios significados y se leerá conforma a la palabra que reemplacé.
  • d) Doble Implicación (?)
La Doble Implicación es un conectivo mas fuerte que la implicación y por ende mas fuerte que la disyunción y conjuncion su símbolo matemático es (?). Tiene su significado correspondiente dentro de las oraciones reemplazara a la palabra Si y Solo Si en las proposiciones y se leerá tal como se lea dicha palabra.
  • e) Disyunción Exclusiva (V)
La disyunción exclusiva dentro de la jerarquía de los conectivos viene a ocupar el primer lugar. Su simbología matemática es una (v) Normal que a diferencia de la disyunción tiene una línea debajo de la (V) lo que por lo tanto permite diferenciarlas. Reemplazara en las oraciones a la palabra O p O q Pero no ambas lo que implica que se tendrá que elegir una sola opción y no las dos al mismo tiempo. Se leerá tal como se pronuncie la palabra correspondiente.

Valores de Verdad de Una Proposición

El valor de verdad de una proposición tiene por objetivo demostrar con que valor de verdad esta actuando una proposición. Este valor puede ser verdadero o falso dependiendo de la veracidad de dicha oración. Se simboliza de la siguiente manera tomando el siguiente significado.
? (P) = F o V "Significa el valor de verdad de la proposición P es igual a F o V"
PROBLEMAS QUE INVOLUCRAN RESOLUCIONES CON PROPOSICIONES
  • a) PROBLEMA TIPO I (Dada una Oración Determinar si es Proposición)
- Determinar si las siguientes Oraciones son Proposiciones
1.- la Gravedad vale 9,81 mt/sg2
Solución
1er paso.- Verificando que tipo de oración es
Es una declaración Declarativa
2do Paso.- Determinar si es Proposición
Es una Proposición por que es una declaración declarativa y por lo tanto se puede decir si es verdadera o falsa
2.- 3+3=9
Solución
1er paso.- Verificando que tipo de oración es
Es una declaración Declarativa
2do Paso.- Determinar si es Proposición
Es una Proposición por que es una declaración declarativa y por lo tanto se puede decir si es verdadera o falsa
3.- Algebra es una materia de primer semestre
Solución
1er paso.- Verificando que tipo de oración es
Es una declaración Declarativa
2do Paso.- Determinar si es Proposición
Es una Proposición por que es una declaración declarativa y por lo tanto se puede decir si es verdadera o falsa
4.- el cielo es de color celeste
Solución
1er paso.- Verificando que tipo de oración es
Es una declaración Declarativa
2do Paso.- Determinar si es Proposición
Es una Proposición por que es una declaración declarativa y por lo tanto se puede decir si es verdadera o falsa
5.- newton fue un famoso químico
Solución
1er paso.- Verificando que tipo de oración es
Es una declaración Declarativa
2do Paso.- Determinar si es Proposición
Es una Proposición por que es una declaración declarativa y por lo tanto se puede decir si es verdadera o falsa
6.- La carrera de Ingeniería Petrolera pertenece a la facultad de Ciencias Económicas
Solución
1er paso.- Verificando que tipo de oración es
Es una declaración Declarativa
2do Paso.- Determinar si es Proposición
Es una Proposición por que es una declaración declarativa y por lo tanto se puede decir si es verdadera o falsa
7.- La materia de algebra I es una materia muy difícil
Solución
1er paso.- Verificando que tipo de oración es
Es una declaración Declarativa
2do Paso.- Determinar si es Proposición
Es una Proposición por que es una declaración declarativa y por lo tanto se puede decir si es verdadera o falsa
8.- las vocales son diez
Solución
1er paso.- Verificando que tipo de oración es
Es una declaración Declarativa
2do Paso.- Determinar si es Proposición
Es una Proposición por que es una declaración declarativa y por lo tanto se puede decir si es verdadera o falsa
9.- El tema de Derivadas pertenece a la materia de Ecuaciones Diferenciales
Solución
1er paso.- Verificando que tipo de oración es
Es una declaración Declarativa
2do Paso.- Determinar si es Proposición
Es una Proposición por que es una declaración declarativa y por lo tanto se puede decir si es verdadera o falsa
10.- En el curso existen más de 100 Alumnos
Solución
1er paso.- Verificando que tipo de oración es
Es una declaración Declarativa
2do Paso.- Determinar si es Proposición
Es una Proposición por que es una declaración declarativa y por lo tanto se puede decir si es verdadera o falsa
11.- 3+3
Solución
1er Paso.- Verificando que tipo de oración es
Es una expresión Matemática sin sentido
2do Paso.- Determinar si es Proposición
No es una proposición por que carece de igualdad por lo tanto no se puede decir si es verdadera o falsa.
12.- Quiero ir a la Plaza
Solución
1er Paso.- Verificando que tipo de oración es
Es una oración de deseo
2do Paso.- Determinar si es Proposición
No es una proposición por que es una oración de Deseo y por lo tanto no tiene sentido afirmar si es verdadera o falsa
13.- Quiero Jugar Cartas
Solución
1er Paso.- Verificando que tipo de oración es
Es una oración de deseo
2do Paso.- Determinar si es Proposición
No es una proposición por que es una oración de Deseo y por lo tanto no tiene sentido afirmar si es verdadera o falsa
14.- Tráeme dos asientos del otro curso por favor
Solución
1er Paso.- Verificando que tipo de Oración es
Es una oración de Orden
2do Paso.- Determinar si es Proposición
No es una Proposición por que es una oración de orden y por lo tanto no tiene sentido afirmar si es verdadera o falsa
15.- Ayúdame a terminar mi tarea
Solución
1er Paso.- Verificando que tipo de Oración es
Es una oración de Orden
2do Paso.- Determinar si es Proposición
No es una Proposición por que es una oración de orden y por lo tanto no tiene sentido afirmar si es verdadera o falsa
16.- ¡Viva Blooming!
Solución
1er Paso.- Verificando que tipo de Oración es
Es una oración de Admiración
2do Paso.- Determinar si es Proposición
No es una Proposición por que es una oración de Admiración y por lo tanto no tiene sentido afirmar si es verdadera o falsa.
17.- ¡Viva Santa Cruz!
Solución
1er Paso.- Verificando que tipo de Oración es
Es una oración de Admiración
2do Paso.- Determinar si es Proposición
No es una Proposición por que es una oración de Admiración y por lo tanto no tiene sentido afirmar si es verdadera o falsa
18.- ¿Cómo es tu Nombre?
Solución
1er Paso.- Verificando que tipo de Oración es
Es una oración de Interrogación
2do Paso.- Determinar si es Proposición
No es una Proposición por que es una oración de Interrogación y por lo tanto no tiene sentido afirmar si es verdadera o falsa
19.- ¿Cuántos años tienes?
Solución
1er Paso.- Verificando que tipo de Oración es
Es una oración de Interrogación
2do Paso.- Determinar si es Proposición
No es una Proposición por que es una oración de Interrogación y por lo tanto no tiene sentido afirmar si es verdadera o falsa
20.- ¿Cuál es tu materia Favorita?
Solución
1er Paso.- Verificando que tipo de Oración es
Es una oración de Interrogación
2do Paso.- Determinar si es Proposición
No es una Proposición por que es una oración de Interrogación y por lo tanto no tiene sentido afirmar si es verdadera o falsa
  • b) PROBLEMA TIPO II (Dadas las proposiciones determinar su expresión simbólica)
- Para solucionar estos problemas se siguen los siguientes pasos
1.- Se lee el pensamiento para determinar cuantas oraciones tiene el mismo
2.- El numero de oraciones estará en función a los conectivos lógicos que se encuentren en el pensamiento es decir y-o-entonces-si y solo si- si P o Q pero no ambas. (Palabras claves)
3.- Una vez determinado el número de oraciones existentes en el pensamiento se procede a nombrar a cada una asignándole un valor a cada una generalmente una letra del alfabeto a partir de la letra P.
4.- Si hubiera oraciones negadas estas deben nombrarse en forma positiva y cuando se tengan que simbolizar se las coloca en forma negativa.
5.- Se procede a escribir el pensamiento en su correspondiente simbología matemática reemplazando las palabras claves por sus respectivos conectivos
NOTA: EN LOS EJERCICIOS A CONTINUACION EL COLOR ROJO MOSTRARA LOS CONECTIVOS QUE SE ENCUENTRAN EN CADA ORACION.
21.- No es cierto que no me gusta bailar
* Solución
* Asignando un valor a la Oración
p = Me gusta bailar
* Formalizando la Oración
~~p
22.- Me gusta bailar y leer libros de ciencia ficción
* Solución
* Asignando un valor para cada Oración
p = Me gusta bailar
q = Leer libros de ciencia ficción
Monografias.com
Monografias.com
Monografias.com
Monografias.com
PROBLEMA TIPO III (Dadas las proposiciones y su simbología correspondiente determinar su correspondiente en lenguaje común)
1.- Se reemplaza los valores correspondientes asignados a cada proposición donde corresponda.
2.- Se procede a escribir su equivalencia en lenguaje comun
Sean p, q y r los siguientes enunciados:
p = Estudiare Matemáticas
q = Iré a mi clase de Computación
r = Estoy de buen humor
Escriba en lenguaje común las oraciones que correspondan a los siguientes enunciados
Monografias.com
* Solución
* Colocando el valor correspondiente a cada proposición
p = Estudiare Matemáticas
q = Iré a mi clase de Computación
* Encontrando su correspondiente en lenguaje común
Monografias.com
Monografias.com
* Solución
* Colocando el valor correspondiente a cada proposición
p = Estudiare Matemáticas
q = Iré a mi clase de Computación
r = Estoy de buen humor
* Encontrando su correspondiente en lenguaje común
Monografias.com
Para los problemas tipo IV, V, VI se necesitara primero hacer una pequeña introducción a los valores de verdad de cada conectivo lógicos para que de esta manera se entienda mejor como se solucionan estos problemas
TABLA DE VALORES DE LOS CONECTIVOS LOGICOS
1.- CONJUNCION (^)
Monografias.com
La conjuncion es verdadera solamente cuando el antecedente p y el consecuente q son también verdaderos como se muestra en su tabla marcado con el color rojo
2.- DISYUNCION (V)
Monografias.com
La disyunción es falsa solamente cuando el antecedente p y el consecuente q son también falsos como se muestra en su tabla marcado con el color rojo
3.- IMPLICACION (?)
Monografias.com
La implicación es falsa solamente cuando el antecedente p es verdadero y el consecuente q es falso como se muestra en su tabla con el color rojo
4.- BICONDICIONAL O DOBLE IMPLICACION (?)
Monografias.com
La doble implicación tiene dos casos especiales será verdadera cuando el antecedente p y el consecuente q tomen ambos valores idénticos como se muestra en su tabla marcado con el color rojo
5.- DISYUNCION EXCLUSIVA (V)
Monografias.com
La disyunción exclusiva resulta ser la negación de la doble implicación ya que será falsa cuando el antecedente p y el consecuente q tomen ambos a la vez valores idénticos como se demuestra con rojo en su tabla de verdad.
FORMULARIO PARA FACIL RESOLUCION DE LOS PROBLEMAS
Para evitar de aprenderse todas las combinaciones mostradas en cada una de las tablas de verdad de los conectivos lógicos se realizara este formulario que permitirá una fácil solución de los problemas
Monografias.com
Por lo tanto el alumno solo debe aprenderse estas siete combinaciones para poder dominar y resolver los problemas que se mostraran a continuación
PROBLEMA TIPO IV (VALORES DE VERDAD CON CONDICIONES)
Monografias.com
* Solución
* Encontrando el valor de las proposiciones cualesquiera
Como las variables q y s son proposiciones cualesquiera esto significa entonces de que nosotros podemos elegir en forma voluntaria el valor que tomara q y s
Por lo tanto elegimos de qué q sea V y s sea F:
q = V
s = F
* Análisis de la condición
El problema tiene una condición la cual es ~ (p ? ~ r) es verdadera significa entonces de que las variables p y r no pueden ser elegidas por nosotros sus valores saldrán de resolver la condición expuesta en el ejercicio
Como se resuelve la condición?
Reemplazando un valor a la variable p y a la variable r de tal manera que cuando se hagan operaciones esta de cómo resultado verdadero aquí entra la aplicación del formulario expuesto anteriormente.
Monografias.com
Por lo tanto para que la conclusión se cumpla Las variables p y r deben tomar los siguientes valores
p = F
r = V
* Reemplazando para encontrar el valor de verdad correspondiente
Como ya hemos encontrado todos los valores correspondientes a las proposiciones procedemos a reemplazarlas en la proposición para encontrar su valor de verdad
Monografias.com
* Solución
Como el problema tiene la misma condición del problema anterior entonces ya conocemos cuanto valen los valores de verdad de cada proposición
p = F
q = V
r = V
s = F
* Reemplazando para encontrar el valor de verdad
Monografias.com
Monografias.com
Monografias.com
Monografias.com
Monografias.com
Monografias.com
Monografias.com
Monografias.com

Introducción a las tablas de verdad

Monografias.com
Es una CONTINGENCIA
Monografias.com
Es una CONTINGENCIA
Monografias.com
Es una TAUTOLOGIA
Monografias.com
Es una CONTRADICCION
Monografias.com
Es una TAUTOLOGIA
Monografias.com
Es una CONTINGENCIA
Monografias.com
Es una ANTITAUTOLOGIA
Monografias.com
* Es una TAUTOLOGIA
Monografias.com
Es una CONTINGENCIA
Monografias.com
Es una CONTINGENCIA
La fórmula que rige las tablas de verdad está en función a la cantidad de letras o variables que tenga la proposición esta fórmula está representada por la siguiente expresión matemática:
Monografias.com
Donde n es la cantidad de variables o letras que posea la formula proposicional, cabe recordar que el número de proposiciones puede ser ilimitado, lo que significa que las tablas de verdad pueden determinar el valor de verdad de cualquier razonamiento lógico sin importar el número de variables que tenga dicho razonamiento, es también importante mencionar que el razonamiento estudiado mediante una tabla de verdad no debe ser cualquiera si no uno que tenga y cumpla con las leyes de la lógica, es decir un pensamiento que tenga claridad y que indique algo aproximado a la realidad.
Monografias.com
Es una CONTINGENCIA
Monografias.com
Es una CONTINGENCIA
Las letras A, B, C etc. que se ven en la parte superior de algunos ejercicios son conocidas como "Auxiliares o pivotes" ya que permiten resumir la realización de un ejercicio es decir pueden representar a una formula extensa que exista en la proposición se colocan encima de la formula a la cual están representando así se sabrá que formula fue designada por una de estas letras en la proposición evitando una solución larga.
Monografias.com



EJERCICIOS PROPUESTOS
SIMPLIFICAR LAS PROPOSICIONES SIGUIENTES:










Los circuitos lógicos

Vamos a ejemplificar la materialización del cálculo proposicional, empleando el más antiguo de los dispositivos que ya fue utilizado para fines lógicos por nuestro sabio ingeniero Leonardo Torres Quevedo14, a finales del siglo XIX, al construir sus máquinas aritméticas y su jugador de ajedréz.
Un circuito es un sistema físico compuesto por varios cables conductores conectados entre si por conectores (o circuito lógico elemental o atómico) de diferente tipo.

\begin{picture}(260,120) % put(0,0)\{ textbullet\} \put(115,0){\textbf{Figura 2}... ...Confenero/negacion.bmp x=4cm y=3cm}} % put(260,120)\{ textbullet\} \end{picture} 
El conector más elemental, es el que corresponde con la identidad (vease figura 2), compuesto por una fuente de energía , y por un elemento biestable, (en nuestro caso un relais), de forma que cuando pasa corriente por el cable 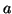$a$ actúa el electroimán haciendo bajar la lengueta, que hace contacto en el borne, dejando pasar la corriente por el cable 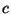$c$, y no pasará corriente por el cable 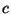$c$ en el caso contrario. Si la proposición 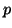$p$ es ``pasa corriente por el cable 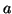$a$" y la proposición 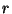$r$ es ``pasa corriente por el cable 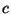$c$", vemos que 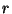$r$ será verdadera cuando 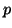$p$ sea verdadera y falsa cuando lo sea 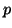$p$. El circuito anterior se comporta como indica la siguiente tabla de verdad: 
Tabla de verdad de la identidad15


$\bf p$$\bf\neg p$
$0$$0$
$1$$1$

De forma análoga se pueden construir conectores que respondan a los operadores de negación (vease figura 2), disyunción (vease figura 3) y conjunción (vease figura 3), cuyas tablas de verdad se indican a continuación:
Tabla de verdad de la negación


$\bf p$$\bf\neg p$
$0$$1$
$1$$0$


Tabla de verdad de la conjunción


$\bf p$$\bf p$${\bf p} {\bf\wedge} {\bf q}$
$0$$0$$0$
$0$$1$$0$
$1$$0$$0$
$1$$1$$1$


Tabla de verdad de la disyunción


$\bf p$$\bf p$${\bf p} {\bf\vee} {\bf q}$
$0$$0$$0$
$0$$1$$1$
$1$$0$$1$
$1$$1$$1$


Estas tablas se materializan mediante los circuitos que representamos en las figuras 2 y 3.

\begin{picture}(260,120) % put(0,0)\{ textbullet\} \put(115,0){\textbf{Figura 3}... ...nfenero/conjuncion.bmp x=4cm y=3cm}} % put(260,120)\{ textbullet\} \end{picture} 
De manera análoga a como se forman proposiciones compuestas a partir de otras proposiciones, se pueden construir los circuitos lógicos compuestos correspondientes a proposiciones compuestas, a partir de loscircuitos lógicos elementales.
Por composición sucesiva se han ido construyendo circuitos cada vez mas complejos hasta llegar a los modernos microprocesadores y otros dispositivos electrónicos componentes de los actuales ordenadores materializados en los microchips que contienen o integran millones de componentes biestables (conectores).
Hemos empleado en nuestra exposición para describir los circuitos elementales un dispositivo electromecánico que fue el precursor de los modernos circuitos electrónicos utilizados en los ordenadores 16. El ingeniero español Torres Quevedo fue el primero en utilizar relais para construir máquinas algebraicas automáticas y otros dispositivos automáticos, como su jugador de ajedrez, superando con ello al matemático inglés Babagge 17, precursor de los actuales ordenadores, pero quien no pudo terminar de construir su maquina por solo disponer para ello de la tecnología mecánica, cuyas componentes eran ruedas y engranajes.
Desde el origen de las computadoras electrónicas, ha habido una sucesión de distintos dispositivos biestables con los que se han construido los conectores lógicos elementales y, a partir de ellos, los circuitos mas complejos componentes de aquellas. En cada época las caracteristicas de los dispositivos usados para construir las nuevas maquinas automáticas, han sido uno de los rasgos empleados para definir las distintas generaciones de ordenadores; esta sucesión de dispositivos pasó del relais a la válvula de radio, y de esta al transistor, para llegar despues a los actuales circuitos integrados cada vez de mayor densidad. Esta sucesión todavia no ha terminado.
Como ya hemos indicado, fue el matemático inglés George Boole el iniciador de la lógica, o cálculo, de proposiciones, pero fue el matemático americano Claude Shannon 18, quien aplicó el álgebra de Boole al diseño de circuitos de conmutacion utilizados en las centrales telefónicas automáticas. Al matemático húngaro John von Neumann 19, se debe la actual estructura de los ordenadores.



Circuitos Lógicos

Es posible expresar las distintas operaciones con proposiciones lógicas mediantecircuitos lógicos, es decir, sistemas donde los valores de verdad se expresan mediante interruptores o abiertos (no pasa la electricidad, falso) o cerrados (pasa la electricidad, verdadero). Las operaciones se expresan de la siguiente manera:
  • La Conjunción: se representa mediante dos interruptores conectados en serie. Si uno de ellos está abierto la electricidad no llega a su destino, lo que se ve reflejado en las tablas de verdad.
  •  La Disyunción Inclusiva: se representa mediante dos interruptores en paralelo, donde le electricidad pasa a menos que los dos estén abiertos, es decir, los dos sean falsos.
  • La Condicional: a partir de las leyes complementarias, podemos definir a la condicional como ~p∨q, por lo que, mediante un circuito lógico quedaría como:
 
  • La bicondicional: mediante las leyes complementarias podemos redefinirla como (p∧q)∨(~p∧~q), entonces:
  • La disyunción exclusiva: finalmente, podemos expresarla mediante leyes complementarias por (p∨q)∧(~p∨~q), por lo que quedaría:
 
Publicado por en No hay comentarios:
Suscribirse a: Comentarios (Atom)